Tutorial on using the BRC algorithm

15 Sep 2024

The branch and bound algorithm for reliability of coherent systems (BRC) algorithm performs system reliability analysis on any general coherent systems.

A coherent system means a system whose state does not deteriorate when a components state improves, which is a common characteristic of many real-world systems.

The figure below illustrates how the BRC algorithm works.

Code demonstration

The jupyter notebook can be found at this BNS-JT GitHub repo.

MBNPy version

The code below is using BNS-JT module’s v1.0.0.

In case the current version of BNS-JT module does not work,
the version can be accessed by

git clone --branch v1.0.0 https://github.com/jieunbyun/BNS-JT

git checkout v1.0.0

import networkx as nx
import matplotlib.pyplot as plt
from BNS_JT import cpm, variable, operation
from networkx.algorithms.flow import shortest_augmenting_path
from BNS_JT import brc
import numpy as np

User input: “coherent” system function

Example: Network with five edges

Network topology

We analyse the network below.

# Network
nodes = {'n1': (0, 0),
         'n2': (1, 1),
         'n3': (1, -1),
         'n4': (2, 0)}

edges = {'e1': ['n1', 'n2'],
	     'e2': ['n1', 'n3'],
	     'e3': ['n2', 'n3'],
	     'e4': ['n2', 'n4'],
	     'e5': ['n3', 'n4']}

%matplotlib inline
plt.figure(figsize=(4,3))
# Draw network
G = nx.Graph()
for node in nodes:
    G.add_node(node, pos=nodes[node])
for e, pair in edges.items():
    G.add_edge(*pair, label=e)

pos = nx.get_node_attributes(G, 'pos')
edge_labels=nx.get_edge_attributes(G, 'label')
nx.draw(G, pos, with_labels=True)
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)
plt.show()

Component events

The state of the five edges are represented by component events.
The edges take binary-state, 0 for non-functional and 1 for functional.

To use the BRC algorithm, component events need to be defined as a variable.Variable object.

varis = {}
for k, v in edges.items():
    varis[k] = variable.Variable( name=k, values = [0, 1]) # values: edge flow capacity

print(varis['e1'])

'Variable(name=e1, B=[{0}, {1}, {0, 1}], values=[0, 1])'

The probabilities of component events are defined as below:

probs = {'e1': {0: 0.01, 1: 0.99}, 'e2': {0: 0.01, 1: 0.99}, 'e3': {0: 0.05, 1: 0.95},
         'e4': {0: 0.05, 1: 0.95}, 'e5': {0: 0.10, 1: 0.90}}

System event

System state is evaluated by network connectivity between a designed origin-destination (OD) pair.
In other words, a system state is survival if the OD pair is connected; and failure otherwise.

This leads to the system function below.
NB1 The first input of a system function must be a dictionary of components state.
NB2 The outputs must be three:

system value: any format (does not affect the BRC algorithm; just for information's sake);
system state: a string, either 's' or 'f'; and
components state that guarantees an obtained system state: a dictionary of affecting components OR (if such information unavailable) None.

def net_conn(comps_st, od_pair, edges, varis): # maximum flow analysis

    G = nx.Graph()
    for k,x in comps_st.items():
        G.add_edge(edges[k][0], edges[k][1]) # we add each edge
        G[edges[k][0]][edges[k][1]]['capacity'] = varis[k].values[x] # define capacity as 0 if state = 0 or 1 if state = 1

    # perform maximum flow analysis between the OD pair
    G.add_edge(od_pair[1], 'new_d', capacity=1) # add a new edge with capacity 1 to ensure we find only ONE path. 
    f_val, f_dict = nx.maximum_flow(G, od_pair[0], 'new_d', capacity='capacity', flow_func=shortest_augmenting_path)

    if f_val > 0: # if the flow between the OD pair is greater than 0, the two nodes are connected
        sys_st = 's'

        # We can infer an associated minimum survival rule in case of network connectivity.
        min_comps_st = {} 
        for k, x in comps_st.items():
            k_flow = max([f_dict[edges[k][0]][edges[k][1]], f_dict[edges[k][1]][edges[k][0]]])
            if k_flow > 0: # the edges with flows > 0 consitute a minimum survival rule.
                min_comps_st[k] = 1

    else:
        sys_st = 'f'

        # In case of system failure, obtaining a minimum failure rule is not straightforward.
        min_comps_st = None

    return f_val, sys_st, min_comps_st

In this example, we consider the OD pair ‘n1’ and ‘n4’.

od_pair=('n1','n4')

To run the BRC algorithm, a system function needs to have only one input components state.

This can be done using a lambda function.

sys_fun = lambda comps_st : net_conn(comps_st, od_pair, edges, varis)

Below are a few examples using the system function.

comps_st = {'e1': 1, 'e2': 1, 'e3': 1, 'e4': 1, 'e5': 1}
f_val, sys_st, min_comps_st = sys_fun(comps_st)
print(f_val, sys_st, min_comps_st)

1 s {'e1': 1, 'e4': 1}

In the result above, the components state leads to system survival.

We also have the survival rule that if e1 and e4 have a state no less than 1, the system survives regardless of the states of other components.

comps_st = {'e1': 0, 'e2': 1, 'e3': 1, 'e4': 1, 'e5': 1}
f_val, sys_st, min_comps_st = sys_fun(comps_st)
print(f_val, sys_st, min_comps_st)

1 s {'e2': 1, 'e5': 1}

This time, we obtain a different survival rule because e1 has state 0 and therefore the previous rule no longer applies.

comps_st = {'e1': 0, 'e2': 0, 'e3': 1, 'e4': 1, 'e5': 1}
f_val, sys_st, min_comps_st = sys_fun(comps_st)
print(f_val, sys_st, min_comps_st)

0 f None

This case leads to system failure with e1 and e2 being dysfunctional.

The minimum failure rule is returned None.

Application of the BRC algorithm

Now we run the BRC algorithm.

Below, we set pf_bnd_wr = 0.0, indicating that the algorithm stops when the bound width on system failure probability is 0.
In other words, the analysis aims for a complete (not approximate) analysis.

We set the other stopping criteria as max_sf=np.inf and max_nb=np.inf.
The variables indicate the maximum number of system function runs and that of created branches
Aiming for a complete analysis, we set both values to infinity.

brs, rules, sys_res, monitor = brc.run(varis, probs, sys_fun, max_sf=np.inf, max_nb=np.inf, pf_bnd_wr=0.0)

*** Analysis completed with f_sys runs 8: out_flag = complete ***
The # of found non-dominated rules (f, s): 8 (4, 4)
Probability of branchs (f, s, u): (5.1688e-03, 9.95e-01, 0.0000e+00)
The # of branches (f, s, u), (min, avg) len of rf: 11 (5, 6, 0), (2, 2.50)

The algorithm stops after running the function 8 times, obtaining system failure probability as $5.16 \cdot 10^{-3}$.

The system function has 4 survival rules and 4 failure rules:

print(rules['s'])
print(rules['f'])

[{'e1': 1, 'e4': 1}, {'e2': 1, 'e5': 1}, {'e2': 1, 'e3': 1, 'e4': 1}, {'e1': 1, 'e3': 1, 'e5': 1}]
[{'e4': 0, 'e5': 0}, {'e1': 0, 'e2': 0}, {'e1': 0, 'e3': 0, 'e5': 0}, {'e2': 0, 'e3': 0, 'e4': 0}]

The system event space is decomposed into 5 failure branches and 6 survival branches.

print(brs[0])

Branch(down={'e1': 1, 'e2': 0, 'e3': 0, 'e4': 1, 'e5': 0}, up={'e1': 1, 'e2': 1, 'e3': 1, 'e4': 1, 'e5': 1}, down_state=s, up_state=s, p=0.9405

One can do further analysis using the branches.

To this end, we can use cpm and variable objects.

from BNS_JT import cpm

varis['sys'] = variable.Variable(name='sys', values=['f', 's']) # state 0 for failure and 1 for survival

# probability distributions using CPM
cpms = {}

# component events
for k, v in edges.items():
    cpms[k] = cpm.Cpm( variables = [varis[k]], no_child=1, C = np.array([[0],[1]]), p=np.array([probs[k][0], probs[k][1]]) )

# system event
Csys, varis = brc.get_csys(brs, varis, {'f': 0, 's': 1})
print(Csys) # each branch becomes a row in the system's event matrix
psys = np.array([1.0]*len(Csys)) # the system function is determinisitic, i.e. all instances have a probability of 1.

cpms['sys'] = cpm.Cpm( [varis['sys']] + [varis[e] for e in edges], 1, Csys, psys )
print(cpms['sys'])

[[1 1 2 2 1 2]
 [1 1 1 2 0 1]
 [1 0 1 1 1 2]
 [0 1 2 2 0 0]
 [0 0 1 1 0 0]
 [1 0 1 1 0 1]
 [0 1 0 0 0 1]
 [1 1 0 1 0 1]
 [1 0 1 0 2 1]
 [0 0 0 2 2 2]
 [0 0 1 0 2 0]]
Cpm(variables=['sys', 'e1', 'e2', 'e3', 'e4', 'e5'], no_child=1, C=[[1 1 2 2 1 2]
 [1 1 1 2 0 1]
 [1 0 1 1 1 2]
 [0 1 2 2 0 0]
 [0 0 1 1 0 0]
 [1 0 1 1 0 1]
 [0 1 0 0 0 1]
 [1 1 0 1 0 1]
 [1 0 1 0 2 1]
 [0 0 0 2 2 2]
 [0 0 1 0 2 0]], p=[[1.]
 [1.]
 [1.]
 [1.]
 [1.]
 [1.]
 [1.]
 [1.]
 [1.]
 [1.]
 [1.]]

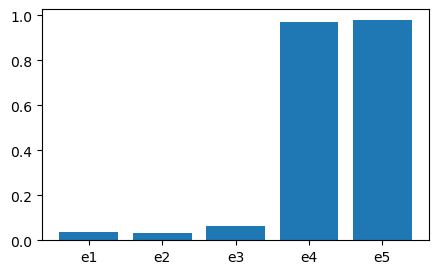
For instance, one can compute component importance
$P(X_n=0 | S=0) = P(X_n=0, S=0) / P(S=0)$ as below.

def get_cim( comp_name, cpms, varis, pf ):
    var_elim_names = list(edges.keys())
    var_elim_names.remove(comp_name)

    var_elim_order = [varis[e] for e in var_elim_names]


    cpm_s_x = operation.variable_elim( cpms, var_elim_order )
    row_idx = np.where((cpm_s_x.C == [0, 0]).all(axis=1))
    p_s0_x0 = sum(cpm_s_x.p[row_idx])

    cim = p_s0_x0[0] / pf

    return cim

cims = {}
for comp_name in edges:
    cims[comp_name] = get_cim( comp_name, cpms, varis, pf = 5.4114e-03 )
print(cims)

fig, ax = plt.subplots(figsize=(5,3))
ax.bar( cims.keys(), cims.values() )
plt.show()

{'e1': 0.03631684961377838, 'e2': 0.03174317182244893, 'e3': 0.059924418819529104, 'e4': 0.9289231991721185, 'e5': 0.9344208522748267}