Expected days of power cut
20 Jul 2024Tags: example max-min-system
This article is based on the jupyter notebook script at MBNPy GitHub respository.
The quantification and inference algorithm below has a complexity of $O(M^{N_p})$, where $M$ is the number of states and $N_p$ is the number of components that constitute paths from a house to substations. In other words, $N_p$ is the major bottleneck. Good news is that however many the total number of structures and houses, what only matters in the end is simply the number of structures on the paths to a house.
COMING SOON: Implementation to a full-scale system.
Modules
import sys
import numpy as np
import random
import copy
import time
import pandas as pd
import matplotlib.pyplot as plt
random.seed(10)
# mbnpy toolkit
sys.path.append(r"C:\Users\jb622s\git\BNS-JT\BNS_JT")
from BNS_JT import cpm, variable, operation
Problem
System
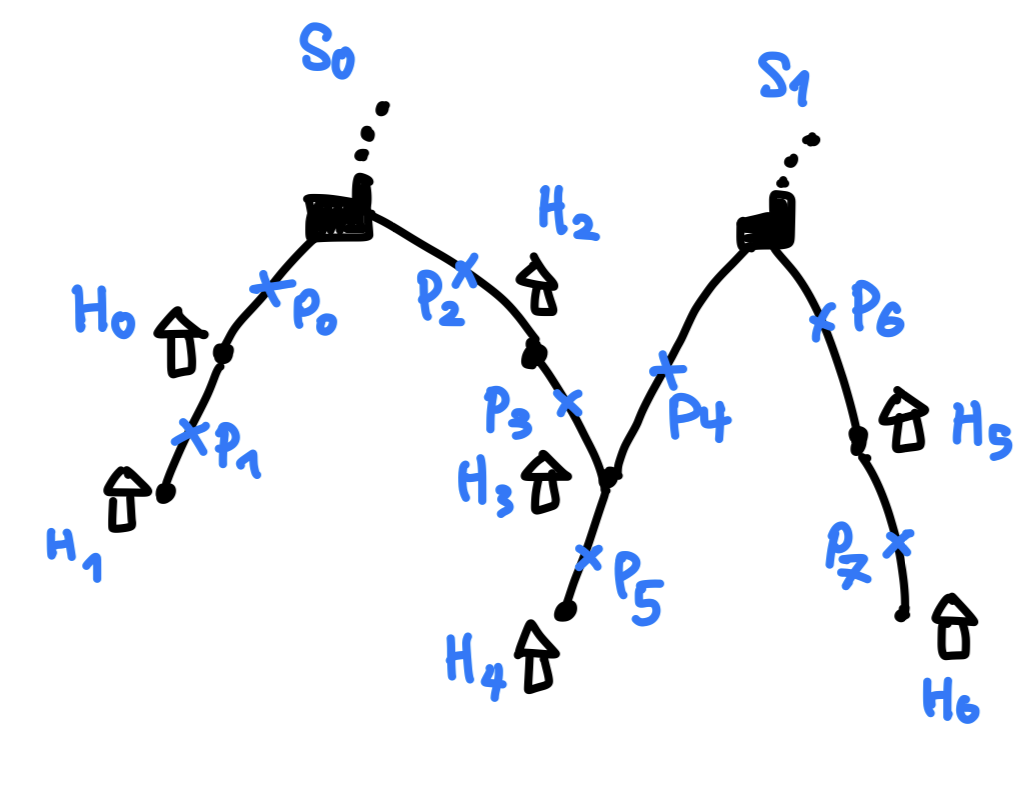
The system consists of two power substations $S_0$ and $S_1$, eight transmission line poles $P_0$, …, $P_7$, and seven houses $H_0$, …, $H_6$. The substations and poles may fail being subjected to hazard scenarios $H$. Once a hazard event occurs, repair works will take place with priorities $S_0$ → $S_1$ → $P_0$ → $P_1$ → … → $P_6$. The works are done only for failed components, and repairing a component takes a day.
Of interest is the expected number of days of power cut for each house. A house has power when the substation and poles it is connected to all survive. For example, $H_0$ has access to power if $S_0$ and $P_0$ are both in operation, while $H_1$ does if $S_0$, $P_0$, and $P_1$ are all in operation. We note that houses $H_3$ and $H_4$ have access to both substations and get power when either of the two link-sets is available. For example, $H_3$ has power either $S_0$, $P_2$, and $P_3$ work together or $S_1$ and $P_4$ are in operation.
Bayesian network (BN) graph
The BN graph can be set up as below:
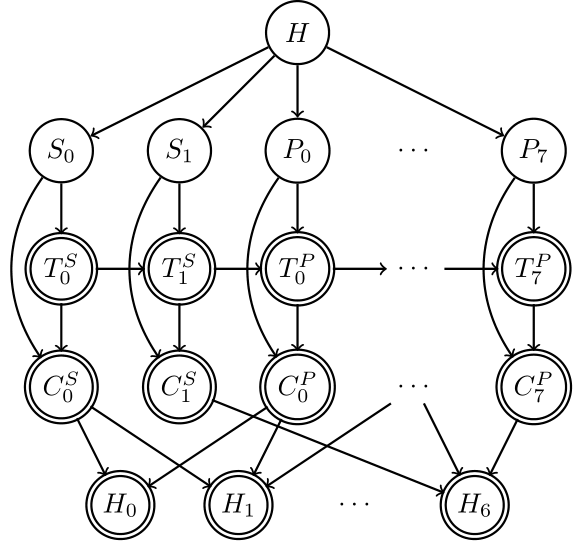
The hazard node $H$ affects damage states of components, $S_0$, $S_1$, $P_0$, …, $P_7$. Then, damage state of a component $X$ decides the rapair timing (i.e. how many days after a hazard occurrence) of a corresponding component, $T^X$. $T^X$ is also affected by the timing of the component right before in the repair priority, e.g. $T_1^S$ is dependent on $T^S_0$ as $S_0$ is right before $S_1$ in the repair priority. Then, actual closure time of each component, $C^X$ is decided by the corresponding damage state $X$ and $T^X$. That is, if $X$ has failed, then the closure time is the same as $T^X$, while if it is not, the closure time is zero. Finally, each house’s duration of power cut, represneted by $H_0$, …, $H_7$, is decided by the closure duration of components constituting their link-sets. For example, as aforementioned, teh first house has $S_0$ and $P_0$ in its link set, and therefore the node $H_0$ is connected to $C_0^S$ and $C^P_0$.
In the graph, random variables are represented by single border, while deterministic variables are represented by double border.
Modelling
Hazard scenarios
cpms={}
vars={}
vars['haz'] = variable.Variable( name='haz', values=['mild','medi','inte'] ) # values=(mild, medium, intense)
cpms['haz'] = cpm.Cpm( variables=[vars['haz']], no_child=1, C=np.array([0,1,2]), p=[0.5,0.2,0.3] )
print(vars['haz'])
print(cpms['haz'])
"Variable(name=haz, B=[{0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2}, {0, 1, 2}], values=['mild', 'medi', 'inte'])"
Cpm(variables=['haz'], no_child=1, C=[[0]
[1]
[2]], p=[[0.5]
[0.2]
[0.3]]
Structural damage
# Substations
n_subs = 2
for i in range(n_subs):
name = 'xs' + str(i)
vars[name] = variable.Variable( name=name, values=['fail','surv'] ) # values=(failure, survival)
cpms[name] = cpm.Cpm( variables = [vars[name], vars['haz']], no_child = 1,
C=np.array([[0,0], [1,0], [0,1], [1,1], [0,2], [1,2]]) )
cpms['xs0'].p = np.array([0.001, 0.999, 0.01, 0.99, 0.1, 0.9])
cpms['xs1'].p = np.array([0.005, 0.995, 0.05, 0.95, 0.2, 0.8])
# Poles
n_pole = 8
for i in range(n_pole):
name = 'xp' + str(i)
vars[name] = variable.Variable( name=name, values=['fail','surv'] ) # values=(failure, survival)
cpms[name] = cpm.Cpm( variables = [vars[name], vars['haz']], no_child = 1,
C=np.array([[0,0], [1,0], [0,1], [1,1], [0,2], [1,2]]) )
if i in [0,2,4,6]:
cpms[name].p = np.array([0.001, 0.999, 0.01, 0.99, 0.1, 0.9])
else:
cpms[name].p = np.array([0.005, 0.995, 0.05, 0.95, 0.2, 0.8])
Repair timing
max_ct = n_subs + n_pole
# Repair priority
rep_pri = ['xs' + str(i) for i in range(n_subs)] + ['xp' + str(i) for i in range(n_pole)] # repair priority
print(rep_pri)
['xs0', 'xs1', 'xp0', 'xp1', 'xp2', 'xp3', 'xp4', 'xp5', 'xp6', 'xp7']
for i, x in enumerate(rep_pri):
name = 't'+x[1:]
vars[name] = variable.Variable( name=name, values=list(range(i+2)), B_flag='store' )
if i < 1: # first element
cpms[name] = cpm.Cpm( variables = [vars[name], vars[x]], no_child = 1, C=np.array([[1,0], [0, 1]]), p=np.array([1,1]) )
else:
t_old_vars = vars[t_old].values
Cx = np.empty(shape=(0,3), dtype=int)
for v in t_old_vars:
Cx_new = [[v, 1, v], [v+1, 0, v]]
Cx = np.vstack( [Cx, Cx_new] )
cpms[name] = cpm.Cpm( variables = [vars[name], vars[x], vars[t_old]], no_child = 1, C=Cx, p=np.ones(shape=(2*len(t_old_vars)), dtype=np.float32) )
t_old = copy.deepcopy(name)
print(vars['ts0'])
print(cpms['ts0'])
print(" ")
print(vars['tp3'])
print(cpms['tp3'])
'Variable(name=ts0, B=[{0}, {1}, {0, 1}], values=[0, 1])'
Cpm(variables=['ts0', 'xs0'], no_child=1, C=[[1 0]
[0 1]], p=[[1]
[1]]
'Variable(name=tp3, B=[{0}, {1}, {2}, {3}, {4}, {5}, {6}, {0, 1}, {0, 2}, {0, 3}, {0, 4}, {0, 5}, {0, 6}, {1, 2}, {1, 3}, {1, 4}, {1, 5}, {1, 6}, {2, 3}, {2, 4}, {2, 5}, {2, 6}, {3, 4}, {3, 5}, {3, 6}, {4, 5}, {4, 6}, {5, 6}, {0, 1, 2}, {0, 1, 3}, {0, 1, 4}, {0, 1, 5}, {0, 1, 6}, {0, 2, 3}, {0, 2, 4}, {0, 2, 5}, {0, 2, 6}, {0, 3, 4}, {0, 3, 5}, {0, 3, 6}, {0, 4, 5}, {0, 4, 6}, {0, 5, 6}, {1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {1, 2, 6}, {1, 3, 4}, {1, 3, 5}, {1, 3, 6}, {1, 4, 5}, {1, 4, 6}, {1, 5, 6}, {2, 3, 4}, {2, 3, 5}, {2, 3, 6}, {2, 4, 5}, {2, 4, 6}, {2, 5, 6}, {3, 4, 5}, {3, 4, 6}, {3, 5, 6}, {4, 5, 6}, {0, 1, 2, 3}, {0, 1, 2, 4}, {0, 1, 2, 5}, {0, 1, 2, 6}, {0, 1, 3, 4}, {0, 1, 3, 5}, {0, 1, 3, 6}, {0, 1, 4, 5}, {0, 1, 4, 6}, {0, 1, 5, 6}, {0, 2, 3, 4}, {0, 2, 3, 5}, {0, 2, 3, 6}, {0, 2, 4, 5}, {0, 2, 4, 6}, {0, 2, 5, 6}, {0, 3, 4, 5}, {0, 3, 4, 6}, {0, 3, 5, 6}, {0, 4, 5, 6}, {1, 2, 3, 4}, {1, 2, 3, 5}, {1, 2, 3, 6}, {1, 2, 4, 5}, {1, 2, 4, 6}, {1, 2, 5, 6}, {1, 3, 4, 5}, {1, 3, 4, 6}, {1, 3, 5, 6}, {1, 4, 5, 6}, {2, 3, 4, 5}, {2, 3, 4, 6}, {2, 3, 5, 6}, {2, 4, 5, 6}, {3, 4, 5, 6}, {0, 1, 2, 3, 4}, {0, 1, 2, 3, 5}, {0, 1, 2, 3, 6}, {0, 1, 2, 4, 5}, {0, 1, 2, 4, 6}, {0, 1, 2, 5, 6}, {0, 1, 3, 4, 5}, {0, 1, 3, 4, 6}, {0, 1, 3, 5, 6}, {0, 1, 4, 5, 6}, {0, 2, 3, 4, 5}, {0, 2, 3, 4, 6}, {0, 2, 3, 5, 6}, {0, 2, 4, 5, 6}, {0, 3, 4, 5, 6}, {1, 2, 3, 4, 5}, {1, 2, 3, 4, 6}, {1, 2, 3, 5, 6}, {1, 2, 4, 5, 6}, {1, 3, 4, 5, 6}, {2, 3, 4, 5, 6}, {0, 1, 2, 3, 4, 5}, {0, 1, 2, 3, 4, 6}, {0, 1, 2, 3, 5, 6}, {0, 1, 2, 4, 5, 6}, {0, 1, 3, 4, 5, 6}, {0, 2, 3, 4, 5, 6}, {1, 2, 3, 4, 5, 6}, {0, 1, 2, 3, 4, 5, 6}], values=[0, 1, 2, 3, 4, 5, 6])'
Cpm(variables=['tp3', 'xp3', 'tp2'], no_child=1, C=[[0 1 0]
[1 0 0]
[1 1 1]
[2 0 1]
[2 1 2]
[3 0 2]
[3 1 3]
[4 0 3]
[4 1 4]
[5 0 4]
[5 1 5]
[6 0 5]], p=[[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]]
Closure time
i=1
name = 'cs' + str(i)
vals = vars['ts'+str(i)].values
#vars[name] = variable.Variable( name=name, values=vals )
print(vals)
st = vars['ts'+str(i)].B.index(set(vals))
print(st)
[0, 1, 2]
6
for x in rep_pri:
name = 'c'+x[1:]
name_t = 't'+x[1:]
vals = vars[name_t].values
vars[name] = variable.Variable( name=name, values=vals, B_flag='store' )
ts_all = vars[name_t].B.index(set(vals))
Cx = np.array([[0, 1, ts_all]])
for v in vals:
if v > 0:
Cx = np.vstack((Cx, [v, 0, v]))
cpms[name] = cpm.Cpm( variables = [vars[name], vars[x], vars[name_t]], no_child = 1, C=Cx, p=np.ones(shape=(len(Cx),1), dtype=np.float32) )
print(vars['cs0'])
print(cpms['cs0'])
print(" ")
print(vars['cp3'])
print(cpms['cp3'])
'Variable(name=cs0, B=[{0}, {1}, {0, 1}], values=[0, 1])'
Cpm(variables=['cs0', 'xs0', 'ts0'], no_child=1, C=[[0 1 2]
[1 0 1]], p=[[1.]
[1.]]
'Variable(name=cp3, B=[{0}, {1}, {2}, {3}, {4}, {5}, {6}, {0, 1}, {0, 2}, {0, 3}, {0, 4}, {0, 5}, {0, 6}, {1, 2}, {1, 3}, {1, 4}, {1, 5}, {1, 6}, {2, 3}, {2, 4}, {2, 5}, {2, 6}, {3, 4}, {3, 5}, {3, 6}, {4, 5}, {4, 6}, {5, 6}, {0, 1, 2}, {0, 1, 3}, {0, 1, 4}, {0, 1, 5}, {0, 1, 6}, {0, 2, 3}, {0, 2, 4}, {0, 2, 5}, {0, 2, 6}, {0, 3, 4}, {0, 3, 5}, {0, 3, 6}, {0, 4, 5}, {0, 4, 6}, {0, 5, 6}, {1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {1, 2, 6}, {1, 3, 4}, {1, 3, 5}, {1, 3, 6}, {1, 4, 5}, {1, 4, 6}, {1, 5, 6}, {2, 3, 4}, {2, 3, 5}, {2, 3, 6}, {2, 4, 5}, {2, 4, 6}, {2, 5, 6}, {3, 4, 5}, {3, 4, 6}, {3, 5, 6}, {4, 5, 6}, {0, 1, 2, 3}, {0, 1, 2, 4}, {0, 1, 2, 5}, {0, 1, 2, 6}, {0, 1, 3, 4}, {0, 1, 3, 5}, {0, 1, 3, 6}, {0, 1, 4, 5}, {0, 1, 4, 6}, {0, 1, 5, 6}, {0, 2, 3, 4}, {0, 2, 3, 5}, {0, 2, 3, 6}, {0, 2, 4, 5}, {0, 2, 4, 6}, {0, 2, 5, 6}, {0, 3, 4, 5}, {0, 3, 4, 6}, {0, 3, 5, 6}, {0, 4, 5, 6}, {1, 2, 3, 4}, {1, 2, 3, 5}, {1, 2, 3, 6}, {1, 2, 4, 5}, {1, 2, 4, 6}, {1, 2, 5, 6}, {1, 3, 4, 5}, {1, 3, 4, 6}, {1, 3, 5, 6}, {1, 4, 5, 6}, {2, 3, 4, 5}, {2, 3, 4, 6}, {2, 3, 5, 6}, {2, 4, 5, 6}, {3, 4, 5, 6}, {0, 1, 2, 3, 4}, {0, 1, 2, 3, 5}, {0, 1, 2, 3, 6}, {0, 1, 2, 4, 5}, {0, 1, 2, 4, 6}, {0, 1, 2, 5, 6}, {0, 1, 3, 4, 5}, {0, 1, 3, 4, 6}, {0, 1, 3, 5, 6}, {0, 1, 4, 5, 6}, {0, 2, 3, 4, 5}, {0, 2, 3, 4, 6}, {0, 2, 3, 5, 6}, {0, 2, 4, 5, 6}, {0, 3, 4, 5, 6}, {1, 2, 3, 4, 5}, {1, 2, 3, 4, 6}, {1, 2, 3, 5, 6}, {1, 2, 4, 5, 6}, {1, 3, 4, 5, 6}, {2, 3, 4, 5, 6}, {0, 1, 2, 3, 4, 5}, {0, 1, 2, 3, 4, 6}, {0, 1, 2, 3, 5, 6}, {0, 1, 2, 4, 5, 6}, {0, 1, 3, 4, 5, 6}, {0, 2, 3, 4, 5, 6}, {1, 2, 3, 4, 5, 6}, {0, 1, 2, 3, 4, 5, 6}], values=[0, 1, 2, 3, 4, 5, 6])'
Cpm(variables=['cp3', 'xp3', 'tp3'], no_child=1, C=[[ 0 1 126]
[ 1 0 1]
[ 2 0 2]
[ 3 0 3]
[ 4 0 4]
[ 5 0 5]
[ 6 0 6]], p=[[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]]
Power cut time
# Example 1
vars_p_h0 = [vars['cp0'], vars['cs0']]
M_h0, v_h0 = operation.sys_max_val('h0', vars_p_h0)
print(M_h0, v_h0)
# Example 2
vars_p_h1 = [vars['cp1'], vars['cp0'], vars['cs0']]
M_h1, v_h1 = operation.sys_max_val('h1', vars_p_h1)
print("")
print(M_h1, v_h1)
Cpm(variables=['h0', 'cp0', 'cs0'], no_child=1, C=[[0 0 0]
[1 1 2]
[2 2 2]
[3 3 2]
[1 0 1]], p=[[1.]
[1.]
[1.]
[1.]
[1.]] 'Variable(name=h0, B=[{0}, {1}, {2}, {3}, {0, 1}, {0, 2}, {0, 3}, {1, 2}, {1, 3}, {2, 3}, {0, 1, 2}, {0, 1, 3}, {0, 2, 3}, {1, 2, 3}, {0, 1, 2, 3}], values=[0, 1, 2, 3])'
Cpm(variables=['h1', 'cp1', 'cp0', 'cs0'], no_child=1, C=[[ 0 0 0 0]
[ 1 1 4 2]
[ 2 2 10 2]
[ 3 3 14 2]
[ 4 4 14 2]
[ 1 0 1 2]
[ 2 5 2 2]
[ 3 15 3 2]
[ 1 0 0 1]], p=[[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]] 'Variable(name=h1, B=[{0}, {1}, {2}, {3}, {4}, {0, 1}, {0, 2}, {0, 3}, {0, 4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {0, 1, 2}, {0, 1, 3}, {0, 1, 4}, {0, 2, 3}, {0, 2, 4}, {0, 3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {0, 1, 2, 3}, {0, 1, 2, 4}, {0, 1, 3, 4}, {0, 2, 3, 4}, {1, 2, 3, 4}, {0, 1, 2, 3, 4}], values=[0, 1, 2, 3, 4])'
cut_lin = {} # cut-set of link-sets for each house
cut_lin['h0'] = [['cs0', 'cp0']]
cut_lin['h1'] = [['cs0', 'cp0', 'cp1']]
cut_lin['h2'] = [['cs0', 'cp2']]
cut_lin['h3'] = [['cs0', 'cp2', 'cp3'], ['cs1','cp4']]
cut_lin['h4'] = [['cs0', 'cp2', 'cp3', 'cp5'], ['cs1', 'cp4','cp5']]
cut_lin['h5'] = [['cs1', 'cp6']]
cut_lin['h6'] = [['cs1', 'cp6', 'cp7']]
for h, sets in cut_lin.items():
if len(sets) == 1:
vars_h = [vars[x] for x in sets[0]]
cpms[h], vars[h] = operation.sys_max_val( h, vars_h )
else:
names_hs = [h+str(i) for i in range(len(sets))]
for h_i, s_i in zip(names_hs, sets):
vars_h_i = [vars[x] for x in s_i]
cpms[h_i], vars[h_i] = operation.sys_max_val( h_i, vars_h_i )
vars_hs = [vars[n] for n in names_hs]
cpms[h], vars[h] = operation.sys_min_val( h, vars_hs )
print(vars['h1'])
print(cpms['h1'])
print("")
print(vars['h3'])
print(cpms['h3'])
print("")
print(vars['h30'])
print(cpms['h30'])
'Variable(name=h1, B=[{0}, {1}, {2}, {3}, {4}, {0, 1}, {0, 2}, {0, 3}, {0, 4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {0, 1, 2}, {0, 1, 3}, {0, 1, 4}, {0, 2, 3}, {0, 2, 4}, {0, 3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {0, 1, 2, 3}, {0, 1, 2, 4}, {0, 1, 3, 4}, {0, 2, 3, 4}, {1, 2, 3, 4}, {0, 1, 2, 3, 4}], values=[0, 1, 2, 3, 4])'
Cpm(variables=['h1', 'cs0', 'cp0', 'cp1'], no_child=1, C=[[ 0 0 0 0]
[ 1 1 4 5]
[ 1 0 1 5]
[ 2 2 2 15]
[ 3 2 3 25]
[ 1 0 0 1]
[ 2 2 4 2]
[ 3 2 10 3]
[ 4 2 14 4]], p=[[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]]
'Variable(name=h3, B=[{0}, {1}, {2}, {3}, {4}, {5}, {6}, {0, 1}, {0, 2}, {0, 3}, {0, 4}, {0, 5}, {0, 6}, {1, 2}, {1, 3}, {1, 4}, {1, 5}, {1, 6}, {2, 3}, {2, 4}, {2, 5}, {2, 6}, {3, 4}, {3, 5}, {3, 6}, {4, 5}, {4, 6}, {5, 6}, {0, 1, 2}, {0, 1, 3}, {0, 1, 4}, {0, 1, 5}, {0, 1, 6}, {0, 2, 3}, {0, 2, 4}, {0, 2, 5}, {0, 2, 6}, {0, 3, 4}, {0, 3, 5}, {0, 3, 6}, {0, 4, 5}, {0, 4, 6}, {0, 5, 6}, {1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {1, 2, 6}, {1, 3, 4}, {1, 3, 5}, {1, 3, 6}, {1, 4, 5}, {1, 4, 6}, {1, 5, 6}, {2, 3, 4}, {2, 3, 5}, {2, 3, 6}, {2, 4, 5}, {2, 4, 6}, {2, 5, 6}, {3, 4, 5}, {3, 4, 6}, {3, 5, 6}, {4, 5, 6}, {0, 1, 2, 3}, {0, 1, 2, 4}, {0, 1, 2, 5}, {0, 1, 2, 6}, {0, 1, 3, 4}, {0, 1, 3, 5}, {0, 1, 3, 6}, {0, 1, 4, 5}, {0, 1, 4, 6}, {0, 1, 5, 6}, {0, 2, 3, 4}, {0, 2, 3, 5}, {0, 2, 3, 6}, {0, 2, 4, 5}, {0, 2, 4, 6}, {0, 2, 5, 6}, {0, 3, 4, 5}, {0, 3, 4, 6}, {0, 3, 5, 6}, {0, 4, 5, 6}, {1, 2, 3, 4}, {1, 2, 3, 5}, {1, 2, 3, 6}, {1, 2, 4, 5}, {1, 2, 4, 6}, {1, 2, 5, 6}, {1, 3, 4, 5}, {1, 3, 4, 6}, {1, 3, 5, 6}, {1, 4, 5, 6}, {2, 3, 4, 5}, {2, 3, 4, 6}, {2, 3, 5, 6}, {2, 4, 5, 6}, {3, 4, 5, 6}, {0, 1, 2, 3, 4}, {0, 1, 2, 3, 5}, {0, 1, 2, 3, 6}, {0, 1, 2, 4, 5}, {0, 1, 2, 4, 6}, {0, 1, 2, 5, 6}, {0, 1, 3, 4, 5}, {0, 1, 3, 4, 6}, {0, 1, 3, 5, 6}, {0, 1, 4, 5, 6}, {0, 2, 3, 4, 5}, {0, 2, 3, 4, 6}, {0, 2, 3, 5, 6}, {0, 2, 4, 5, 6}, {0, 3, 4, 5, 6}, {1, 2, 3, 4, 5}, {1, 2, 3, 4, 6}, {1, 2, 3, 5, 6}, {1, 2, 4, 5, 6}, {1, 3, 4, 5, 6}, {2, 3, 4, 5, 6}, {0, 1, 2, 3, 4, 5}, {0, 1, 2, 3, 4, 6}, {0, 1, 2, 3, 5, 6}, {0, 1, 2, 4, 5, 6}, {0, 1, 3, 4, 5, 6}, {0, 2, 3, 4, 5, 6}, {1, 2, 3, 4, 5, 6}, {0, 1, 2, 3, 4, 5, 6}], values=[0, 1, 2, 3, 4, 5, 6])'
Cpm(variables=['h3', 'h30', 'h31'], no_child=1, C=[[ 0 0 254]
[ 1 1 253]
[ 2 2 245]
[ 3 3 217]
[ 4 4 161]
[ 5 5 91]
[ 6 6 35]
[ 0 125 0]
[ 1 118 1]
[ 2 97 2]
[ 3 62 3]
[ 4 27 4]
[ 5 6 5]], p=[[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]]
'Variable(name=h30, B=[{0}, {1}, {2}, {3}, {4}, {5}, {6}, {0, 1}, {0, 2}, {0, 3}, {0, 4}, {0, 5}, {0, 6}, {1, 2}, {1, 3}, {1, 4}, {1, 5}, {1, 6}, {2, 3}, {2, 4}, {2, 5}, {2, 6}, {3, 4}, {3, 5}, {3, 6}, {4, 5}, {4, 6}, {5, 6}, {0, 1, 2}, {0, 1, 3}, {0, 1, 4}, {0, 1, 5}, {0, 1, 6}, {0, 2, 3}, {0, 2, 4}, {0, 2, 5}, {0, 2, 6}, {0, 3, 4}, {0, 3, 5}, {0, 3, 6}, {0, 4, 5}, {0, 4, 6}, {0, 5, 6}, {1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {1, 2, 6}, {1, 3, 4}, {1, 3, 5}, {1, 3, 6}, {1, 4, 5}, {1, 4, 6}, {1, 5, 6}, {2, 3, 4}, {2, 3, 5}, {2, 3, 6}, {2, 4, 5}, {2, 4, 6}, {2, 5, 6}, {3, 4, 5}, {3, 4, 6}, {3, 5, 6}, {4, 5, 6}, {0, 1, 2, 3}, {0, 1, 2, 4}, {0, 1, 2, 5}, {0, 1, 2, 6}, {0, 1, 3, 4}, {0, 1, 3, 5}, {0, 1, 3, 6}, {0, 1, 4, 5}, {0, 1, 4, 6}, {0, 1, 5, 6}, {0, 2, 3, 4}, {0, 2, 3, 5}, {0, 2, 3, 6}, {0, 2, 4, 5}, {0, 2, 4, 6}, {0, 2, 5, 6}, {0, 3, 4, 5}, {0, 3, 4, 6}, {0, 3, 5, 6}, {0, 4, 5, 6}, {1, 2, 3, 4}, {1, 2, 3, 5}, {1, 2, 3, 6}, {1, 2, 4, 5}, {1, 2, 4, 6}, {1, 2, 5, 6}, {1, 3, 4, 5}, {1, 3, 4, 6}, {1, 3, 5, 6}, {1, 4, 5, 6}, {2, 3, 4, 5}, {2, 3, 4, 6}, {2, 3, 5, 6}, {2, 4, 5, 6}, {3, 4, 5, 6}, {0, 1, 2, 3, 4}, {0, 1, 2, 3, 5}, {0, 1, 2, 3, 6}, {0, 1, 2, 4, 5}, {0, 1, 2, 4, 6}, {0, 1, 2, 5, 6}, {0, 1, 3, 4, 5}, {0, 1, 3, 4, 6}, {0, 1, 3, 5, 6}, {0, 1, 4, 5, 6}, {0, 2, 3, 4, 5}, {0, 2, 3, 4, 6}, {0, 2, 3, 5, 6}, {0, 2, 4, 5, 6}, {0, 3, 4, 5, 6}, {1, 2, 3, 4, 5}, {1, 2, 3, 4, 6}, {1, 2, 3, 5, 6}, {1, 2, 4, 5, 6}, {1, 3, 4, 5, 6}, {2, 3, 4, 5, 6}, {0, 1, 2, 3, 4, 5}, {0, 1, 2, 3, 4, 6}, {0, 1, 2, 3, 5, 6}, {0, 1, 2, 4, 5, 6}, {0, 1, 3, 4, 5, 6}, {0, 2, 3, 4, 5, 6}, {1, 2, 3, 4, 5, 6}, {0, 1, 2, 3, 4, 5, 6}], values=[0, 1, 2, 3, 4, 5, 6])'
Cpm(variables=['h30', 'cs0', 'cp2', 'cp3'], no_child=1, C=[[ 0 0 0 0]
[ 1 1 6 7]
[ 1 0 1 7]
[ 2 2 2 28]
[ 3 2 3 63]
[ 4 2 4 98]
[ 5 2 5 119]
[ 1 0 0 1]
[ 2 2 6 2]
[ 3 2 21 3]
[ 4 2 41 4]
[ 5 2 56 5]
[ 6 2 62 6]], p=[[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]
[1.]]
Inference
We apply conditioning on $H$ and variable elimination (VE) on other variables. For VE, we need to decide elimination order as $S_0$ → $T_0^S$ → $C^S_0$ → $S_1$ → $T_1^S$ → $C^S_1$ → $P_0$ → … → $C_7^P$ → $H_0$ → $H_1$ → … → $H_6$.
n_hou = len(cut_lin)
VE_ord= ['haz']
for x in rep_pri:
VE_ord.append(x)
VE_ord.append('t'+x[1:])
VE_ord.append('c'+x[1:])
VE_ord += ['h0', 'h1', 'h2']+['h30', 'h31', 'h3']+['h40', 'h41', 'h4'] + ['h5', 'h6']
Then, if we want to obtain the marginal distribution of $H_n$, $P(H_n)$ by summing out all other variables, we only need to consider those variables that are (grand, great grand, etc.) parents of $H_n$.
For example, in case of $H_0$, we have those relevant variables as marked blue in the figure below:

The set of those relevant variables can be obtained using the function cpm.get_inf_vars, as shown in the code below:
# Example 1
h_star1 = ['h0']
vars_inf1 = operation.get_inf_vars( cpms, h_star1, VE_ord )
print(vars_inf1)
# Example 2
h_star2 = ['h0','h1']
vars_inf2 = operation.get_inf_vars( cpms, h_star2, VE_ord )
print(vars_inf2)
['haz', 'xs0', 'ts0', 'cs0', 'xs1', 'ts1', 'xp0', 'tp0', 'cp0', 'h0']
['haz', 'xs0', 'ts0', 'cs0', 'xs1', 'ts1', 'xp0', 'tp0', 'cp0', 'xp1', 'tp1', 'cp1', 'h0', 'h1']
Now we perform inference.
Below, we calcualte $P(H_0)$ by first obtaining an inference scope (i.e. variables to consider) using cpm.get_inf_vars and executing the conditioning-VE algorithm by cpm.cal_Msys_by_cond_VE.
cond_names = ['haz']
# H0
vars_inf_h0 = operation.get_inf_vars( cpms, ['h0'], VE_ord )
ve_names = [x for x in vars_inf_h0 if x not in cond_names]
Msys_h0 = operation.variable_elim_cond([cpms[k] for k in ve_names], [vars[v] for v in ve_names if v != 'h0'],
[cpms[k] for k in cond_names])
print(Msys_h0)
print(sum(Msys_h0.p))
Cpm(variables=['h0'], no_child=1, C=[[0]
[1]
[2]
[3]], p=[[9.38020500e-01]
[5.34575025e-02]
[7.92099500e-03]
[6.01002500e-04]]
[1.]
We now calculate $P(H_6)$, which takes much longer than $H_0$ (in my desktop, it takes 30 seconds). This is because we now have more variables to consider because $T_7^P$ is in the last priority of repair, and thus all $T_x$ becomes relevant. The variables in the inference scope are marked below in the figure below:

One might consider applying sampling instead of the applied exact inference for faster calculation or a larger number of components (i.e. substations and poles).
# H6
vars_inf_h6 = operation.get_inf_vars( cpms, ['h6'], VE_ord )
ve_names = [x for x in vars_inf_h6 if x not in cond_names]
Msys_h6 = operation.variable_elim_cond([cpms[k] for k in ve_names], [vars[v] for v in ve_names if v != 'h6'],
[cpms[k] for k in cond_names])
print(Msys_h6)
print(sum(Msys_h6.p))
Cpm(variables=['h6'], no_child=1, C=[[ 0]
[ 1]
[ 2]
[ 3]
[ 4]
[ 5]
[ 6]
[ 7]
[ 8]
[ 9]
[10]], p=[[8.46012488e-01]
[8.37913635e-02]
[3.87747064e-02]
[2.13166722e-02]
[7.92699644e-03]
[1.86292686e-03]
[2.84743240e-04]
[2.82798049e-05]
[1.76064092e-06]
[6.24000037e-08]
[9.60000006e-10]]
[1.]
Final result
We now calculate for all houses.
cond_names = ['haz']
VE_ord= ['haz']
for x in rep_pri:
VE_ord.append(x)
VE_ord.append('t'+x[1:])
VE_ord.append('c'+x[1:])
VE_ord += ['h0', 'h1', 'h2']+['h30', 'h31', 'h3']+['h40', 'h41', 'h4'] + ['h5', 'h6']
Mhs = {}
for h in cut_lin.keys():
st = time.time()
vars_inf = operation.get_inf_vars( cpms, [h], VE_ord )
ve_names = [x for x in vars_inf if x not in cond_names]
Mhs[h] = operation.variable_elim_cond([cpms[k] for k in ve_names],
[vars[v] for v in ve_names if v != h],
[cpms[k] for k in cond_names])
en = time.time()
print( h + " Done. " + "Took {:.2f} sec.".format(en-st) )
h0 Done. Took 0.10 sec.
h1 Done. Took 0.31 sec.
h2 Done. Took 0.35 sec.
h3 Done. Took 36.69 sec.
h4 Done. Took 176.22 sec.
h5 Done. Took 8.59 sec.
h6 Done. Took 39.84 sec.
Using function cpm.get_means, the average number of days of power cut can be calculated.
avg_cut_days = {}
for h in cut_lin.keys():
days = Mhs[h].get_means( [h] )
avg_cut_days[h] = days[0]
print(avg_cut_days)
{'h0': 0.07110250000000003, 'h1': 0.1549099875, 'h2': 0.08022550000000005, 'h3': 0.03758214298500002, 'h4': 0.16464348097007506, 'h5': 0.1408909975000001, 'h6': 0.26823448751250006}
Mapping
To better understand the risks, we map the failure probabilities of structures (i.e. substations and poles) and the average number of affected days for houses.
# Locations for mapping
xdist, ydist = 0.8, 1.0
locs = {"h0": (-xdist, -ydist), "h1": (-2*xdist, -2*ydist), "h2": (xdist, -ydist), "h3": (2*xdist, -2*ydist), "h4": (xdist, -3*ydist), "h5": (5*xdist,-2*ydist), "h6": (6*xdist, -3*ydist)}
locs["s0"], locs["s1"] = (0.0, 0.0), (3.5*xdist, 0.0)
conn = {"p0": ('s0', 'h0'), "p1": ('h0', 'h1'), "p2": ('s0', 'h2'), "p3": ('h2', 'h3'), "p4": ('s1', 'h3'), "p5": ('h3', 'h4'), "p6": ('s1', 'h5'), "p7": ('h5', 'h6')}
for i in range(n_pole):
p = 'p' + str(i)
locs[p] = tuple( [0.5*sum(tup) for tup in zip(locs[conn[p][0]], locs[conn[p][1]])] )
# Gather data
cd_df = pd.DataFrame(columns=['name', 'loc_x', 'loc_y', 'avg_cut_days']) # cut days
for h in cut_lin.keys():
cd_df = pd.concat( [cd_df, pd.DataFrame( [[h, locs[h][0], locs[h][1], avg_cut_days[h]]], columns=cd_df.columns )], ignore_index = True )
fr_df = pd.DataFrame( columns=['name', 'loc_x', 'loc_y', 'pf'] ) # failure probabilities
for i in range(n_subs):
x = 'xs' + str(i)
xs = 's' +str(i)
Mx = cpm.cal_Msys_by_cond_VE( cpms, vars, ['haz'], VE_ord, x )
pf = cpm.get_prob( Mx, [x], [0] )
fr_df = pd.concat( [fr_df, pd.DataFrame([[xs, locs[xs][0], locs[xs][1], pf]], columns=fr_df.columns)], ignore_index=True )
for i in range(n_pole):
x = 'xp' + str(i)
xs = 'p'+str(i)
Mx = cpm.cal_Msys_by_cond_VE( cpms, vars, ['haz'], VE_ord, x )
pf = cpm.get_prob( Mx, [x], [0] )
fr_df = pd.concat( [fr_df, pd.DataFrame([[xs, locs[xs][0], locs[xs][1], pf]], columns=fr_df.columns)], ignore_index=True )
print(cd_df, '\n')
print(fr_df)
name loc_x loc_y avg_cut_days
0 h0 -0.8 -1.0 0.071103
1 h1 -1.6 -2.0 0.154910
2 h2 0.8 -1.0 0.080226
3 h3 1.6 -2.0 0.037582
4 h4 0.8 -3.0 0.164643
5 h5 4.0 -2.0 0.140891
6 h6 4.8 -3.0 0.268234
name loc_x loc_y pf
0 s0 0.0 0.0 0.0325
1 s1 2.8 0.0 0.0725
2 p0 -0.4 -0.5 0.0325
3 p1 -1.2 -1.5 0.0725
4 p2 0.4 -0.5 0.0325
5 p3 1.2 -1.5 0.0725
6 p4 2.2 -1.0 0.0325
7 p5 1.2 -2.5 0.0725
8 p6 3.4 -1.0 0.0325
9 p7 4.4 -2.5 0.0725
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
for x, pair in conn.items():
loc0, loc1 = locs[pair[0]], locs[pair[1]]
plt.plot([loc0[0], loc1[0]], [loc0[1], loc1[1]], color='grey')
plt.scatter(cd_df['loc_x'].to_list(), cd_df['loc_y'].to_list(), c = cd_df['avg_cut_days'].to_list(), cmap='Reds', s=200, marker="X")
cb1 = plt.colorbar()
cb1.ax.set_xlabel('Avg. \n cut days', size = 15)
plt.scatter(fr_df['loc_x'].to_list(), fr_df['loc_y'].to_list(), c = fr_df['pf'].to_list(), cmap='Reds')
cb2 = plt.colorbar()
cb2.ax.set_xlabel('Fail. \n prob.', size = 15)
tx, ty = 0.10, 0.01
for i, name in enumerate(cd_df['name'].to_list()):
ax.text(cd_df['loc_x'][i]+tx, cd_df['loc_y'][i]+ty, name)
for i, name in enumerate(fr_df['name'].to_list()):
ax.text(fr_df['loc_x'][i]+tx, fr_df['loc_y'][i]+ty, name)
ax.set_xticks([])
ax.set_yticks([])
plt.show()
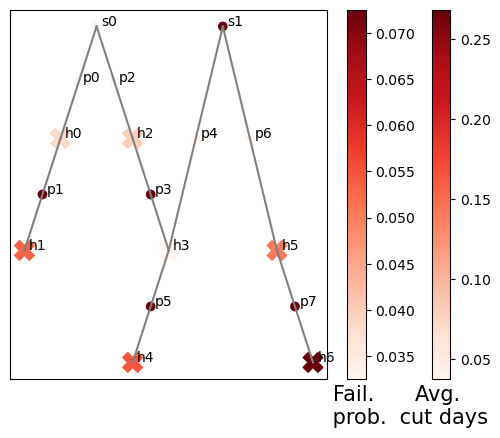
The figure above shows how the convolution of hazard risks, structural performance, and repair priority decides risks faced by houses.
For example, $H_1$ and $H_5$ show similar risk levels. $H_1$ is farther away from substation than $H_5$ but is connected to structures with higher repair priority. The two factors appear to compensate each other.
$H_3$ has the least risk being connected to both substations. Compared to $H_0$, the effect of such redundancy seems dominating other factors, i.e. structural performance and repair priority.